01 Introduction 02 Physical experiments 03 Digital tools 04 Process 05 Results 06 Evaluation 07 Physical models 08 Conclusions

Slender multistress driven structures Guillem Baraut Mattia Gambardella

INTRODUCTION Slender structures, like suspension bridges, use primarily tension to carry both the design loads and their own weight and are generally optimal in that the primary structural elements are not subject to buckling. The need to avoid long compressive spans is critical in determining the optimal form of such structures. Natural systems also use prestressing and as much elements in tension as possible as an strategy to avoid buckling stability problems. All those natural systems are using fibers as a material system for being the cheapest way to introduce tensile structural members in terms of manufacturing time and energy. All natural systems are the results of thousands of generations of an evolutionary system. This long process has been optimising the performance of every single element. Genetic algorithms are the most powerful tools that have been developed that can reproduce this processes of optimization, but they are difficult to implement, and need a very powerful machine. Instead of that, there are similar processes but far more simple that can produce satisfactory results. Actual design methodologies doesnít consider any optimization process because are time consuming and need experts in many fields. The way the majority of design practices work is to create a team that exchanges a lot of information between them, but there is no one person that controls every single aspect of that. This complex work system can be improved if the proper tools are being used. The more expertise work in a team, the more important is the good exchange of information. AIM AND SCOPE OF THE RESEARCH The aim of our research is to define a design methodology that combines the stress driven form finding with a fiber distribution in structures to create a framework that includes both physical and digital form finding tools. Within this framework we will be able to process all the environmental information including external loads to design an optimized structure. The structural evaluation will be embedded in the design process since it integrates the structure optimization. This optimization will be considered from several points of view such as shape, size and topological optimization. Another criteria that will be used in this design methodology is the circulation of people within the structure. Other spatial criteria will be then negotiating with the structural performance. For these purposes some digital tools will be developed to allow the user to have a good level of control over all these criteria. At the end these tools will be tested. The results will be compared within themselves and with existing structures, and several evaluation criteria will be set and analysed. 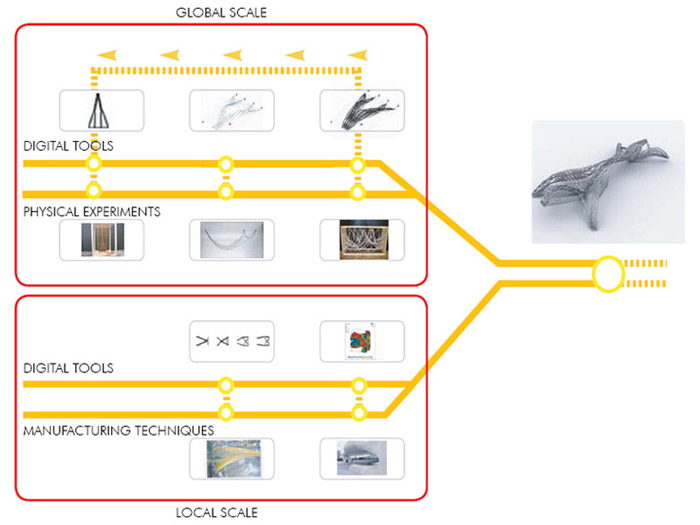HYPOTHESIS Slender lightweight structures could be achieved with optimal distribution of fibers in a system which topology has been defined through an automatic process of optimization. From both architectural and engineering point of view lightweight long span structures will be studied in two scales of operation: - Macroscale based in the overall shape of the structure (metres) - Microscale based in heterogeneity and anisotropic distribution of fibers considering directionality and density (centimetres) Both scales of operation can be defined by stress driven form finding processes.