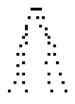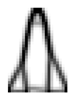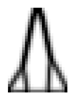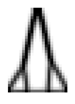01 Introduction 02 Physical experiments 03 Digital tools 04 Process 05 Results 06 Evaluation 07 Physical models 08 Conclusions

Slender multistress driven structures Guillem Baraut Mattia Gambardella

MINIMAL PATH The next set of digital experiments are exploring several ways of defining the minimal paths from an origin to an end point, using some attractors and repellors to determine the area of the flow, but without fixing it. The flow paths can be classified in these classes: - Vector field: when the flow is going from known origin and end points and is affected by the environment (other attractors and repellors) - L-system: The flow is originated in a certain point and certain direction, and is affected by the environment (other attractors and repellors). This flow is going to a broader space in each iteration in order to search the final point. This search is defined according the Lindenmayer system rules, dividing the flow in branches. The combination of both systems can give us a mixed flow between searching and browsing in the space in order to join the origin point with the final one. This end point can be either an attractor, creating a more hierarchical or searching flow paths, or a simple point, making the flow more random-like, or more similar to browsing. In between these points there will be placed other attractors creating interest for some points in the space, and repellors, creating the necessary voids. These voids will determine the spans for the structure and the spaces where the structure cannot be placed. 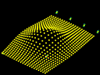TOPOLOGY OPTIMIZATION The topology optimization method solves the problem of distributing a given amount of material in a design domain subject to load and boundary conditions, such that the stiffness of the structure is maximized. This method gained popularity and is being applied to many different fields of design. The aim of this digital experiment is to use the method for complex structural design. This method can improve design cost and quality. The start point of this experiment is the article ëA 99 line topology optimization code written in Matlabí, by O. Sigmund (Department of Solid Mechanics, Technical University of Denmark). The code written in Matlab has been adapted for our purposes in terms of inputs and the way we treat the results, how we export the information to other software, and how we change the parameters according to either the results of other software or even the Matlab results. At the end the 99 line code turned into a 320 lines code, including options for exporting data to excel, text files, generative components, or even command script files for Rhino with the options of lines in 3D and triangulated meshes in 2D and 3D.